DFS / BFS Algorithm

DFS / BFS

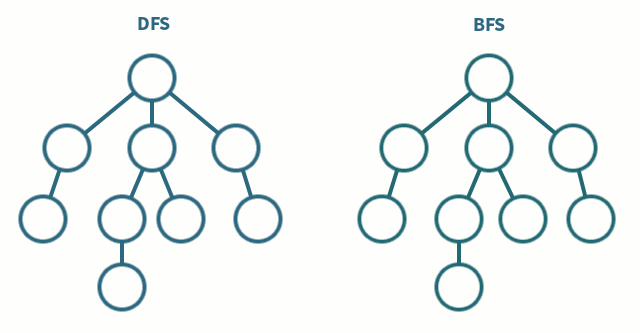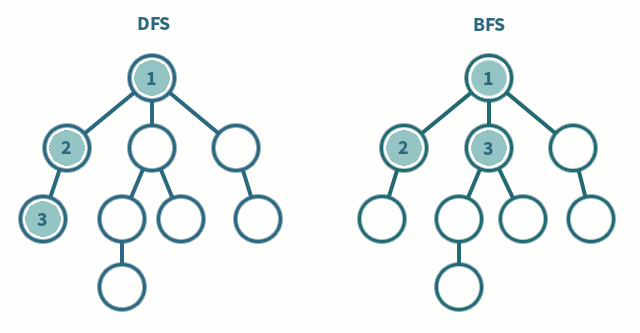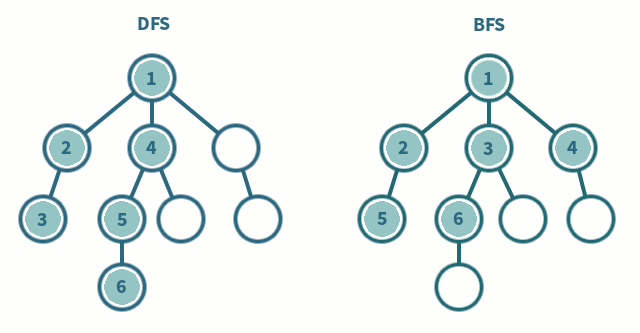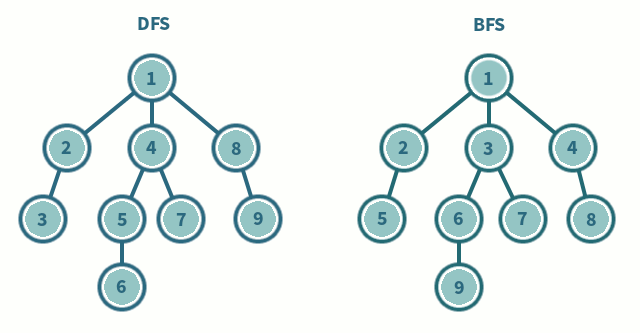
그래프는 정점의 구성 뿐만 아니라 간선의 연결에도 규칙이 존재하지 않기 때문에 탐색이 복잡하다. 따라서 그래프의 모든 정점을 탐색하기 위한 방법은 다음의 두 가지 알고리즘을 기반으로 한다.

깊이 우선 탐색(Depth First Search: DFS)

그래프 상에 존재하는 임의의 한 정점으로부터 연결되어 있는 한 정점으로만 나아간다라는 방법을 우선으로 탐색한다. 일단 연결된 정점으로 탐색하는 것이다.

연결할 수 있는 정점이 있을 때까지 계속 연결하다가 더이상 연결되지 않은 정점이 없으면 바로 그 전 단계의 정점으로 돌아가서 연결할 수 있는 정점이 있는지 살펴봐야 할 것이다. 갔던 길을 되돌아 오는 상황이 존재하는 미로찾기처럼 구성하면 되는 것이다.

어떤 자료구조를 사용해야할까? 바로 Stack 이다. Time Complexity : O(V+E) … vertex 개수 + edge 개수

너비 우선 탐색(Breadth First Search: BFS)

그래프 상에 존재하는 임의의 한 정점으로부터 연결되어 있는 모든 정점으로 나아간다. Tree 에서의 Level Order Traversal 형식으로 진행되는 것이다.

BFS 에서는 자료구조로 Queue 를 사용한다. 연락을 취할 정점의 순서를 기록하기 위한 것이다. 우선, 탐색을 시작하는 정점을 Queue 에 넣는다.(enqueue) 그리고 dequeue 를 하면서 dequeue 하는 정점과 간선으로 연결되어 있는 정점들을 enqueue 한다. 즉 vertex 들을 방문한 순서대로 queue 에 저장하는 방법을 사용하는 것이다.

Time Complexity : O(V+E) … vertex 개수 + edge 개수 ! BFS 로 구한 경로는 최단 경로이다.